Homogeneous Coordinate In Rendering
Homogeneous coordinate is a coordinate system that mapping coordinates in $R^n$ space to $R^{n+1}$ space, there are many methods of mapping but the most commonly used one is using $(x_1,y_1,z_1)=(w x_2, w y_2, w z_2)$, and in $R^{n+1}$ space we will have $(x_2,y_2,z_2,\lambda)$.
The benefits of this transformation come from two aspect and it is best to think of them as two different applications of homogeneous coordinate (we typically using projection matrix to convert the first one to the second one, but the $w$ value here means exactly different things, please don’t mix up):
-
In Cartesian coordinate system, we use the same method to represent points and vectors as $(x,y,z)$, but we actually care about the different between points and vectors in many way, so in this case, we introduce a homogeneous coordinate in $R^4$ represented as $(x,y,z,w)$, with $w\in{0,1}$, for vectors we have $w=0$ and $w=1$ for points, by doing this, we maintain the properties of calculations:
- Subtraction of two points will produce a vector as $1-1=0$.
- Addition of a point and a vector will produce a point as $1+0=1$.
- Addition of two vectors still a vector as $0+0=0$.
Another benefit for Cartesian coordinate system is for basic three transformation: rotation, scaling and translation, we can perform matrix multiplication for rotation and scaling, but translation need to be done in matrix addition. By introducing homogeneous coordinate, we can do translation by matrix multiplication. Why is it a benefit? Well in $R^3$, the transformation can be calculated by $R\times S \times Matrix+T$, we can accelerate it by storing $R\times S$ and the calculation can be done in $O(2)$, but in $R^4$, the transformation is calculated by $T\times R\times S\times Matrix$, it will only takes $O(1)$, it might be insignificant for CPU, but for a GPU unit (GPU is fast because it has a large amount of unit), it is very helpful. Also, when a translation transformation is applied to a vector, it does not affect anything since $w=0$, it is logical because vectors have only direction and magnitude, no position.
-
In projective space, two parallel line is intersect at a far distance:

However it is impossible in Cartesian coordinate system, so we introduction homogeneous coordinate in $R^4$ and the $w$ here indicate the distance from the camera to the point, the further it is, the larger $w$. After transform a very far point form $R^3$ to $R^4$ by $(x_1,y_1,z_1)=(w x_2, w y_2, w z_2)$, since $w$ is very large, $(x_2,y_2,z_2)$ will be very close to 0, and this can be applied to any point that are very far, since all of them has $(x,y,z)=(0,0,0)$ so they are identical, then every parallel lines that extend away from the camera will intersect at such point.
In computer graphics, the $w$ coordinate in projective space is calculated using perspective projection matrix, and it is proportional to $z$ in Cartesian coordinate system (it has literally nothing to do with the $w$ in camera space in Cartesian coordinate system), it indicate the distance from a point to the camera in Cartesian coordinate system. Why do I say it is proportional to $z$? For any points in camera space, suppose we have point $(x,y,z,1)$, we transform it to projective space by calculate the cross product of the projective projection matrix with this point: $$ \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\\ 0 & 1 & 0 & 0 \\\ 0 & 0 & 1 & 0 \\\ 0 & 0 & -1 & 0 \end{array} \right ] \times \left[\begin{matrix} x\\\ y \\\ z \\\ 1\end{matrix}\right] $$
We only care about $w$ so we don’t actually care about the value in the first, second and third row, anyway, the value of new $w$ will be $-z$, however, in OpenGL we are using a right handed world space, which means the further the point goes, the smaller $z$ it is, and the $-z$ will become bigger.
Some tutorial suggest that when $w$ are very close to 0, it can be used to indicated a point at infinity, it is ture and I will discuss it later in Homogeneous Divide in Projective Space.
The symbol using below: $C_n$ means coordinate in NDC, $C_{cl}$ means coordinate in clip space, $C_{ca}$ means camera space.
As mentioned in previous blog, projective projection and orthographic projection will produce two different clip space (they are the same in some way, but here let’s just foces on the appearance).
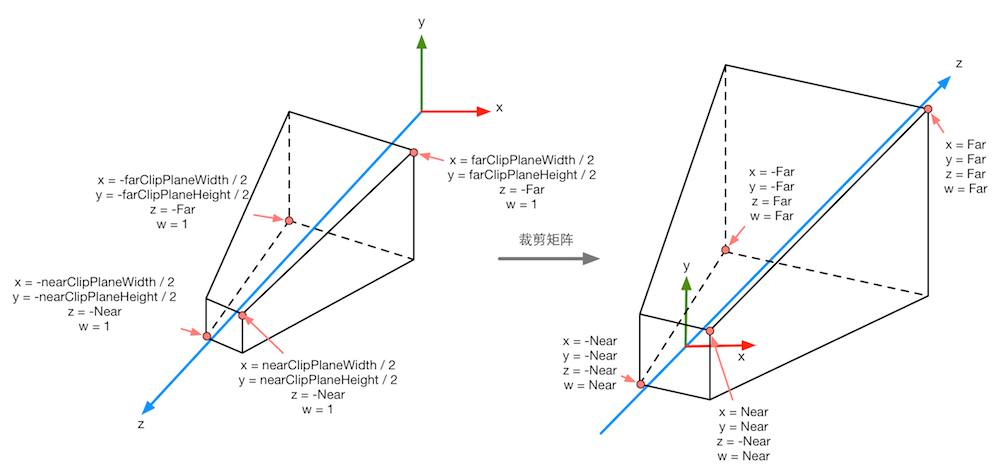
For projective projection:
For orthographic projection:
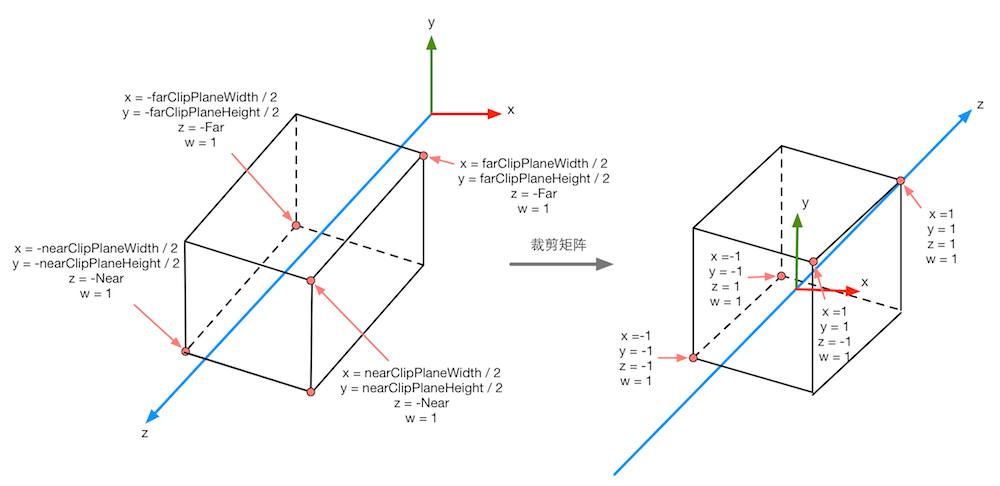
Forget orthographic right now, let’s focus on projective, how do we know that the clip space of perspective projection will looks this way? I strongly suggest this article of deducing the projection matrix used in OpenGL, author tried to squeeze a frustum into NDC cube, but for the projective matrix we obtain at the end, it dismisses the part of divide by $-z_e$ for $x$, $y$ and $z$, where $w_{cl}=-z_{ca}$ as I shown, so we have such relationship between clip space and NDC: $\frac{x_{cl}}{w_{cl}}=x_n,\frac{y_{cl}}{w_{cl}}=y_n,\frac{z_{cl}}{w_{cl}}=z_n$. Attention here: in transformation from camera space to clip space, we also flipping the z-axis, the camera space is using right handed coordinate which means when a object moving toward the forward direction of camera, the value of $z$ decreases, in clip space, the value will increases.
After applied to the perspective projection matrix, we obtain frustum as shown above, but for screen mapping, we need a cube in NDC, to do this we need Projective Division.
Homogeneous Divide in Projective Space
It takes two steps to turn a frustum into a cube, the first step as shown above is turn frustum into a better frustum, the second step is turn this better frustum into cube. In the deduction of projection matrix, we remove the part that divide by $w$ for $x$, $y$, $z$ and we obtain the better frustum we are saying, what if we add them back? The answer is very obvious, by using $\frac{x_{cl}}{w_{cl}}=x_n,\frac{y_{cl}}{w_{cl}}=y_n,\frac{z_{cl}}{w_{cl}}=z_n$ we can quickly turn the better frustum into NDC.
Back to the question before, why a point is at infinity when $w_{cl}$ is 0? For $x$ and $y$ it is easy to understand because $\frac{x_{cl}}{0}=\infty,\frac{y_{cl}}{0}=\infty$ but for $z$ it becomes more confusing because $z_n$ has something to do with $w_n$ since $-z_{ca}=w_{cl}$, we might think when $w_{cl}$ is close to 0, $z_n=\frac{z_{cl}}{w_{cl}}$ should also close to $0$, but it is not true, check the relation between $z_{cl}$ and $z_{ca}$: $$ z_{cl}=-\frac{f+n}{f-n}z_{ca}-\frac{2fn}{f-n} $$ So $z_n$ will become: $$ z_{n}=\frac{f+n}{f-n}+\frac{2fn}{(f-n)*z_{ca}} $$ So it will also go to infinite.
The projective division will be automatically execute by OpenGL after projection (it will also perform for orthographic projection but for this one since $w_{cl}=1$ in any case, it doesn’t matter), there might be clipping between these two steps, someone suggest clipping might happen after division but they are using the same properties, do it isn’t important.
I also found a interesting website while writing this blog: https://webglfundamentals.org/webgl/lessons/webgl-3d-perspective.html